Python Fortran ロゼッタストーン#
NumPyを使用したPythonとFortranは、表現力と機能の点で非常に似ています。このロゼッタストーンは、両方の言語で多くの一般的なイディオムを並べて実装する方法を示しています。
コードスニペットを実行する方法#
たとえば、次のコードスニペットを考えてみましょう
Pythonでは、コードをファイルexample.pyに保存し、python example.pyを使用して実行するだけです。Fortranでは、それをファイルexample.f90に保存し、ファイルの最後にend行を追加します(これがどのように機能するかについての詳細は、モジュールのセクションを参照してください)。gfortran example.f90を使用してコンパイルし、./a.outを使用して実行します(もちろん、gfortranにコンパイルオプションを追加して、別の名前の実行可能ファイルを生成することもできます)。
配列#
配列はFortranに組み込まれており、PythonのNumPyモジュールで利用できます。使い方は同じですが、次の点が異なります。
Fortranは(デフォルトで)1から数えますが、NumPyは常に0から数えます
Fortranの配列セクション(スライス)には両端が含まれますが、NumPyでは始点は含まれ、終点は除外されます
Cでは、配列はメモリに行方向に格納されます(デフォルトでNumPyはCストレージを使用します)。一方、Fortranでは列方向に格納されます(これは次の2つのポイントでのみ重要です)。
デフォルトでは、
reshapeはFortranではFortran順序を使用し、NumPyではC順序を使用します(どちらの場合も、オプションの引数orderを使用して他の順序を使用できます)。これは、reshapeが平坦化などの他の操作で暗黙的に使用される場合にも重要です。最初のインデックスはFortranで最も高速ですが、NumPyでは最後のインデックスが最も高速です
デフォルトでは、NumPyは2次元配列をきれいに表示しますが、Fortranではそれを表示する形式を指定する必要があります(また、Fortranは列方向に表示するため、行方向に表示するには配列を転置する必要があります)
その他はすべて同じで、特に
NumPyとFortranの配列操作の間には1対1の対応があり、両方の言語で同じように簡単に/自然に表現できます
2次元配列の場合、最初のインデックスは行インデックス、2番目のインデックスは列インデックスです(数学の場合と同じです)
NumPy配列とFortran配列は、形状が同じで、同じインデックスに対応する要素が同じであれば同等です(内部メモリストレージが何であるかは関係ありません)
a**2 + 2*a + exp(a)、sin(a)、a * b、a + bなど、数学関数を含む任意の配列式が許可されます(要素ごとに演算します)。行列乗算を使用して2つの行列を乗算するには、関数を使用する必要があります
高度なインデックス作成/スライス
配列は、任意の整数型、実数型、または複素数型にできます
…
from numpy import array, size, shape, min, max, sum
a = array([1, 2, 3])
print(shape(a))
print(size(a))
print(max(a))
print(min(a))
print(sum(a))
integer :: a(3)
a = [1, 2, 3]
print *, shape(a)
print *, size(a)
print *, maxval(a)
print *, minval(a)
print *, sum(a)
end program
from numpy import reshape
a = reshape([1, 2, 3, 4, 5, 6], (2, 3))
b = reshape([1, 2, 3, 4, 5, 6], (2, 3), order="F")
print(a[0, :])
print(a[1, :])
print()
print(b[0, :])
print(b[1, :])
integer :: a(2, 3), b(2, 3)
a = reshape([1, 2, 3, 4, 5, 6], [2, 3], order=[2, 1])
b = reshape([1, 2, 3, 4, 5, 6], [2, 3])
print *, a(1, :)
print *, a(2, :)
print *
print *, b(1, :)
print *, b(2, :)
end program
[1 2 3]
[4 5 6]
[1 3 5]
[2 4 6]
1 2 3
4 5 6
1 3 5
2 4 6
from numpy import array, size, shape, max, min
a = array([[1, 2, 3], [4, 5, 6]])
print(shape(a))
print(size(a, 0))
print(size(a, 1))
print(max(a))
print(min(a))
print(a[0, 0], a[0, 1], a[0, 2])
print(a[1, 0], a[1, 1], a[1, 2])
print(a)
integer :: a(2, 3)
a = reshape([1, 2, 3, 4, 5, 6], [2, 3], order=[2, 1])
print *, shape(a)
print *, size(a, 1)
print *, size(a, 2)
print *, maxval(a)
print *, minval(a)
print *, a(1, 1), a(1, 2), a(1, 3)
print *, a(2, 1), a(2, 2), a(2, 3)
print "(3i5)", transpose(a)
end program
(2, 3)
2
3
6
1
1 2 3
4 5 6
[[1 2 3]
[4 5 6]]
2 3
2
3
6
1
1 2 3
4 5 6
1 2 3
4 5 6
from numpy import array, all, any
i = array([1, 2, 3])
all(i == [1, 2, 3])
any(i == [2, 2, 3])
integer :: i(3)
i = [1, 2, 3]
all(i == [1, 2, 3])
any(i == [2, 2, 3])
from numpy import array, empty
a = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
b = empty(10)
b[:] = 0
b[a > 2] = 1
b[a > 5] = a[a > 5] - 3
integer :: a(10), b(10)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
where (a > 5)
b = a - 3
elsewhere (a > 2)
b = 1
elsewhere
b = 0
end where
end program
from numpy import array, empty
a = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
b = empty(10)
for i in range(len(a)):
if a[i] > 5:
b[i] = a[i] - 3
elif a[i] > 2:
b[i] = 1
else:
b[i] = 0
integer :: a(10), b(10)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
where (a > 5)
b = a - 3
elsewhere (a > 2)
b = 1
elsewhere
b = 0
end where
end program
from numpy import array, sum, ones, size
a = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
print(sum(a))
print(sum(a[(a > 2) & (a < 6)]))
o = ones(size(a), dtype="int")
print(sum(o[(a > 2) & (a < 6)]))
integer :: a(10)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print *, sum(a)
print *, sum(a, mask=a > 2 .and. a < 6)
print *, count(a > 2 .and. a < 6)
end program
from numpy import array, dot
a = array([[1, 2], [3, 4]])
b = array([[2, 3], [4, 5]])
print(a * b)
print(dot(a, b))
integer :: a(2, 2), b(2, 2)
a = reshape([1, 2, 3, 4], [2, 2], order=[2, 1])
b = reshape([2, 3, 4, 5], [2, 2], order=[2, 1])
print *, a * b
print *, matmul(a, b)
end program
[[ 2 6]
[12 20]]
[[10 13]
[22 29]]
2 12 6 20
10 22 13 29
from numpy import array, pi
a = array([i for i in range(1, 7)])
b = array([(2*i*pi+1)/2 for i in range(1, 7)])
c = array([i for i in range(1, 7) for j in range(1, 4)])
use types, only: dp
use constants, only: pi
integer :: a(6), c(18)
real(dp) :: b(6)
integer :: i, j
a = [ (i, i = 1, 6) ]
b = [ ((2*i*pi+1)/2, i = 1, 6) ]
c = [ ((i, j = 1, 3), i = 1, 6) ]
インデックス作成の例#
最初のn個の要素
最後のn個の要素
iとjの間の要素を選択する(両端を含む)
インデックスiから始まるn個の要素を選択する
-n, ..., nの間の要素を選択する
(両端を含む)
配列全体をループする
3番目から7番目の要素の間をループする(両端を含む)
インデックスiとjで文字列を3つの部分に分割し、その部分は次のようになります
ラプラス更新
モジュール#
FortranとPythonのimport文の比較
以下のPython文には、Fortranに相当するものはありません。
FortranモジュールはPythonモジュールと同様に機能します。違い
Fortranモジュールはネストできません(つまり、すべてトップレベルです。一方、Pythonでは、
__init__.pyファイルを使用してモジュールを任意にネストできます)。Pythonの
import Aに相当するFortranの機能はありません。Fortranでは、プライベートモジュールシンボルを指定できます。
同一の機能
モジュールには、変数、型、関数/サブルーチンが含まれています。
デフォルトでは、すべての変数/型/関数は他のモジュールからアクセスできますが、どのシンボルをプライベートまたはパブリックにするかを明示的に指定することで、これを変更できます(Pythonでは、これは暗黙的なインポートでのみ機能します)。
パブリックなシンボルはグローバル名前空間を汚染しませんが、それらを使用するにはモジュールから明示的にインポートする必要があります。
モジュールにシンボルをインポートすると、そのモジュールの一部になり、他のモジュールからインポートできるようになります。
明示的なインポートまたは暗黙的なインポートを使用できます(明示的なインポートを推奨します)。
モジュールを作成します。
そして、メインプログラムから次のように使用します。
Fortranでは、行program mainを省略できます。また、end programの代わりにendでファイルを終了することもできます。そうすれば、最後にendを追加するだけで、任意のコードスニペットをテストできます。
どのシンボルをパブリックとプライベートにするかを指定するには、次のようにします。
__all__ = ["i", "f"]
i = 5
def f(x):
return x + 5
def g(x):
return x - 5
module a
implicit none
private
public i, f
integer :: i = 5
contains
integer function f(x) result(r)
integer, intent(in) :: x
r = x + 5
end function
integer function g(x) result(r)
integer, intent(in) :: x
r = x - 5
end function
end module
ただし、違いがあります。Fortranでは、シンボルgはプライベートになります(明示的なインポートまたは暗黙的なインポートを使用しても、他のモジュールからインポートすることはできません)。fとiはパブリックです。Pythonでは、暗黙的なインポートを使用すると、シンボルgはインポートされませんが、明示的なインポートを使用すると、シンボルgをインポートできます。
浮動小数点数#
NumPyとFortranの両方で、指定された任意の精度で動作でき、精度が指定されていない場合は、デフォルトのプラットフォーム精度が使用されます。
Pythonでは、デフォルトの精度は通常、倍精度ですが、Fortranでは単精度です。関連するPythonおよびNumPyのドキュメントも参照してください。
Fortranでは、_dpサフィックスを使用して精度を常に指定するのが習慣です。ここで、dpは、以下のtypes.f90モジュールでinteger, parameter :: dp=kind(0.d0)として定義されています(必要に応じて1か所で精度を変更できるようにするため)。精度が指定されていない場合は、単精度が使用されます(そのため、単精度/倍精度の破損につながります)。そのため、精度を常に指定する必要があります。
以下のすべてのFortranコードスニペットでは、use types, only: dpを実行したと仮定します。types.f90モジュールは次のとおりです。
module types
implicit none
private
public dp, hp
integer, parameter :: dp=kind(0.d0), & ! double precision
hp=selected_real_kind(15) ! high precision
end module
数学と複素数#
Fortranには組み込みの数学関数がありますが、Pythonではmathモジュールまたは(より高度な関数については)SciPyパッケージからインポートする必要があります。Fortranには定数が含まれていないため、constants.f90モジュール(以下に含めます)を使用する必要があります。
それ以外は、使い方は同じです。
Fortranモジュールconstants.f90
module constants
use types, only: dp
implicit none
private
public pi, e, I
! Constants contain more digits than double precision, so that
! they are rounded correctly:
real(dp), parameter :: pi = 3.1415926535897932384626433832795_dp
real(dp), parameter :: e = 2.7182818284590452353602874713527_dp
complex(dp), parameter :: I = (0, 1)
end module
文字列と書式設定#
PythonとFortranの両方の機能はほぼ同等ですが、構文が少し異なります。
PythonとFortranの両方で、文字列は"または'のいずれかで区切ることができます。
書式設定された文字列を印刷するには、3つの一般的な方法があります。
print("Integer", 5, "and float", 5.5, "works fine.")
print("Integer " + str(5) + " and float " + str(5.5) + ".")
print("Integer %d and float %f." % (5, 5.5))
use utils, only: str
print *, "Integer", 5, "and float", 5.5, "works fine."
print *, "Integer " // str(5) // " and float " // str(5.5_dp) // "."
print '("Integer ", i0, " and float ", f0.6, ".")', 5, 5.5
そして、よく使用される形式をいくつか紹介します。
ネストされた関数#
PythonとFortranの両方で、外側の関数の名前空間にアクセスできるネストされた関数を使用できます。
次のように使用します。
コンテキストを渡すためにコールバックでネストされた関数を使用できます。
def simpson(f, a, b):
return (b-a) / 6 * (f(a) + 4*f((a+b)/2) + f(b))
def foo(a, k):
def f(x):
return a*sin(k*x)
print(simpson(f, 0., pi))
print(simpson(f, 0., 2*pi))
real(dp) function simpson(f, a, b) result(s)
real(dp), intent(in) :: a, b
interface
real(dp) function f(x)
use types, only: dp
implicit none
real(dp), intent(in) :: x
end function
end interface
s = (b-a) / 6 * (f(a) + 4*f((a+b)/2) + f(b))
end function
subroutine foo(a, k)
real(dp) :: a, k
print *, simpson(f, 0._dp, pi)
print *, simpson(f, 0._dp, 2*pi)
contains
real(dp) function f(x) result(y)
real(dp), intent(in) :: x
y = a*sin(k*x)
end function f
end subroutine foo
次のように使用します。
ループでの制御フロー#
PythonとFortranの一般的なループタイプは、それぞれforループとdoループです。どちらの言語でも、単一のループをスキップしたり、ループの実行を停止したりできますが、それを行うためのステートメントは異なります。
breakおよびexitステートメント#
Pythonでは、breakは最も内側のループの実行を停止するために使用されます。Fortranでは、これはexitステートメントで実現されます。名前付きループの場合、exitステートメントに名前を追加することで、どのループが影響を受けるかを指定できます。そうでない場合、最も内側のループが中断されます。
Pythonのexit()は、プログラムまたはインタラクティブセッションの実行を中断します。
continueおよびcycleステートメント#
Pythonのcontinueステートメントは、ループ本体の残りをスキップするために使用されます。その後、ループは次の反復サイクルで続行されます。Fortranのcontinueステートメントは何もせず、代わりにcycleを使用する必要があります。名前付きループの場合、cycleステートメントに名前を追加することで、どのループが影響を受けるかを指定できます。
例#
マンデルブロ集合#
NumPyで記述され、Fortranに変換された実際のプログラムを次に示します。
import numpy as np
ITERATIONS = 100
DENSITY = 1000
x_min, x_max = -2.68, 1.32
y_min, y_max = -1.5, 1.5
x, y = np.meshgrid(np.linspace(x_min, x_max, DENSITY),
np.linspace(y_min, y_max, DENSITY))
c = x + 1j*y
z = c.copy()
fractal = np.zeros(z.shape, dtype=np.uint8) + 255
for n in range(ITERATIONS):
print("Iteration %d" % n)
mask = abs(z) <= 10
z[mask] *= z[mask]
z[mask] += c[mask]
fractal[(fractal == 255) & (~mask)] = 254. * n / ITERATIONS
print("Saving...")
np.savetxt("fractal.dat", np.log(fractal))
np.savetxt("coord.dat", [x_min, x_max, y_min, y_max])
program Mandelbrot
use types, only: dp
use constants, only: I
use utils, only: savetxt, linspace, meshgrid
implicit none
integer, parameter :: ITERATIONS = 100
integer, parameter :: DENSITY = 1000
real(dp) :: x_min, x_max, y_min, y_max
real(dp), dimension(DENSITY, DENSITY) :: x, y
complex(dp), dimension(DENSITY, DENSITY) :: c, z
integer, dimension(DENSITY, DENSITY) :: fractal
integer :: n
x_min = -2.68_dp
x_max = 1.32_dp
y_min = -1.5_dp
y_max = 1.5_dp
call meshgrid(linspace(x_min, x_max, DENSITY), &
linspace(y_min, y_max, DENSITY), x, y)
c = x + I*y
z = c
fractal = 255
do n = 1, ITERATIONS
print "('Iteration ', i0)", n
where (abs(z) <= 10) z = z**2 + c
where (fractal == 255 .and. abs(z) > 10) fractal = 254 * (n-1) / ITERATIONS
end do
print *, "Saving..."
call savetxt("fractal.dat", log(real(fractal, dp)))
call savetxt("coord.dat", reshape([x_min, x_max, y_min, y_max], [4, 1]))
end program
Python版を実行するには、PythonとNumPyが必要です。Fortran版を実行するには、types.f90、constants.f90、およびutils.f90 がFortran-utilsパッケージから必要です。どちらのバージョンも同等のfractal.datファイルとcoord.datファイルを生成します。
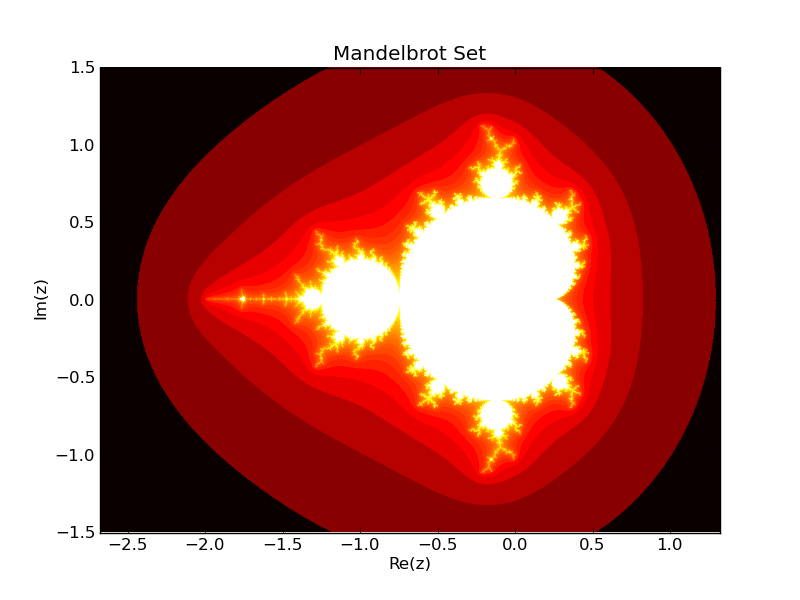
生成されたフラクタルは、以下で表示できます(matplotlibが必要です)。
from numpy import loadtxt
import matplotlib.pyplot as plt
fractal = loadtxt("fractal.dat")
x_min, x_max, y_min, y_max = loadtxt("coord.dat")
plt.imshow(fractal, cmap=plt.cm.hot,
extent=(x_min, x_max, y_min, y_max))
plt.title('Mandelbrot Set')
plt.xlabel('Re(z)')
plt.ylabel('Im(z)')
plt.savefig("mandelbrot.png")
Acer 1830T(gFortran 4.6.1)でのタイミングは以下のとおりです。
Python |
Fortran |
スピードアップ |
|
|---|---|---|---|
計算 |
12.749 |
00.784 |
16.3倍 |
保存 |
01.904 |
01.456 |
1.3倍 |
合計 |
14.653 |
02.240 |
6.5倍 |
最小二乗フィッティング#
PythonではSciPy経由でMinpackを使用し、FortranではMinpackを直接使用します。まず、関数find_fitを持つモジュールfind_fit_moduleを作成します。
from numpy import array
from scipy.optimize import leastsq
def find_fit(data_x, data_y, expr, pars):
data_x = array(data_x)
data_y = array(data_y)
def fcn(x):
return data_y - expr(data_x, x)
x, ier = leastsq(fcn, pars)
if (ier != 1):
raise Exception("Failed to converge.")
return x
module find_fit_module
use minpack, only: lmdif1
use types, only: dp
implicit none
private
public find_fit
contains
subroutine find_fit(data_x, data_y, expr, pars)
real(dp), intent(in) :: data_x(:), data_y(:)
interface
function expr(x, pars) result(y)
use types, only: dp
implicit none
real(dp), intent(in) :: x(:), pars(:)
real(dp) :: y(size(x))
end function
end interface
real(dp), intent(inout) :: pars(:)
real(dp) :: tol, fvec(size(data_x))
integer :: iwa(size(pars)), info, m, n
real(dp), allocatable :: wa(:)
tol = sqrt(epsilon(1._dp))
m = size(fvec)
n = size(pars)
allocate(wa(m*n + 5*n + m))
call lmdif1(fcn, m, n, pars, fvec, tol, info, iwa, wa, size(wa))
if (info /= 1) stop "failed to converge"
contains
subroutine fcn(m, n, x, fvec, iflag)
integer, intent(in) :: m, n, iflag
real(dp), intent(in) :: x(n)
real(dp), intent(out) :: fvec(m)
! Suppress compiler warning:
fvec(1) = iflag
fvec = data_y - expr(data_x, x)
end subroutine
end subroutine
end module
次に、素数のリストに対して、a*x*log(b + c*x)の形式の非線形フィッティングを見つけるためにそれを使用します。
from numpy import size, log
from find_fit_module import find_fit
def expression(x, pars):
a, b, c = pars
return a*x*log(b + c*x)
y = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 53, 59, 61, 67, 71]
pars = [1., 1., 1.]
pars = find_fit(range(1, size(y)+1), y, expression, pars)
print(pars)
program example_primes
use find_fit_module, only: find_fit
use types, only: dp
implicit none
real(dp) :: pars(3)
real(dp), parameter :: y(*) = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, &
37, 41, 43, 47, 53, 59, 61, 67, 71]
integer :: i
pars = [1._dp, 1._dp, 1._dp]
call find_fit([(real(i, dp), i=1,size(y))], y, expression, pars)
print *, pars
contains
function expression(x, pars) result(y)
real(dp), intent(in) :: x(:), pars(:)
real(dp) :: y(size(x))
real(dp) :: a, b, c
a = pars(1)
b = pars(2)
c = pars(3)
y = a*x*log(b + c*x)
end function
end program
これは以下を出力します。
1.4207732655565537 1.6556111085593115 0.53462502018670921